初心者がブログを書くとどうなるの②初めに行う設定編
櫻井 司冴
つかさの教室
クラス替えで好きな人と同じクラスになる確率の求め方！小学生から高校生まで計算方法を解説
櫻井 司冴
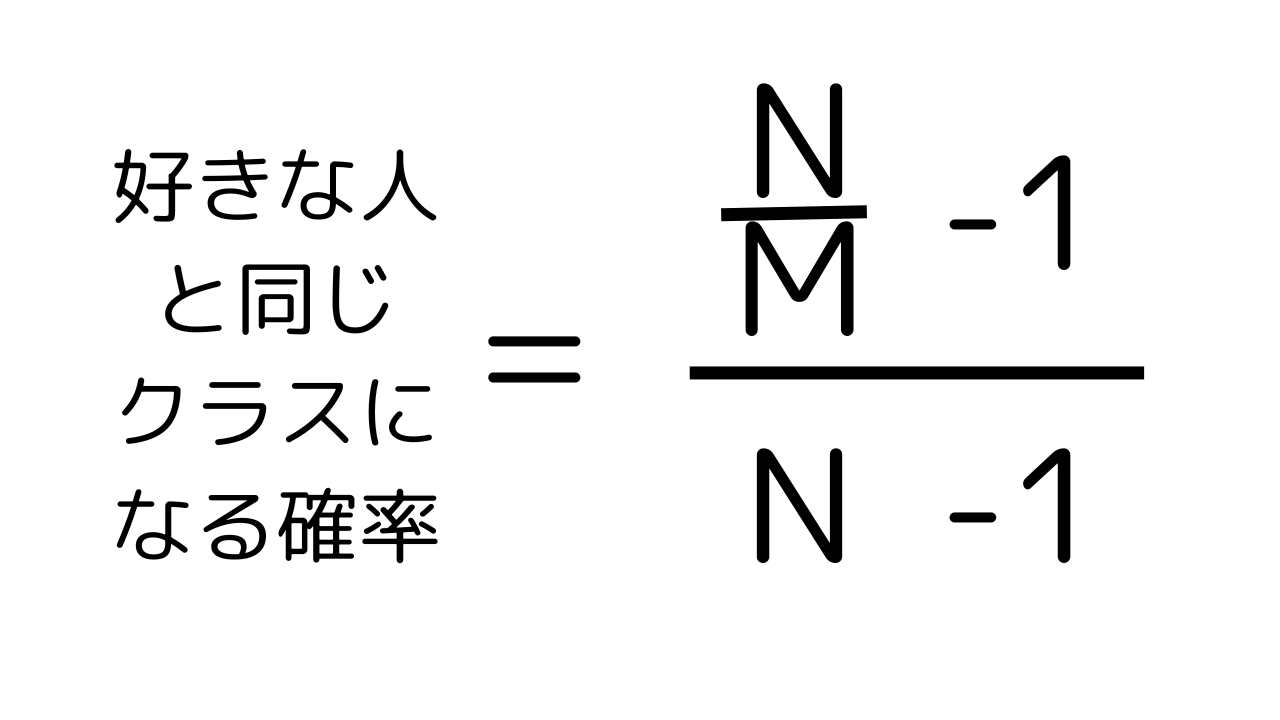
こんにちは、つかさの教室の教室長つかさです。
あの人と3年間同じクラスだ、運命かも…って思うことないですか？どのくらいで起こる確率なのか解説していきたいと思います。
もくじ
今回の設定
好きな人が一人いるとします。性別は同じでも違っていてもいいです。その人と同じになるのはどれくらいの確率なのか計算していきます。
同じクラスになるおおよその確率(小学生向け)
2組しかない時で考えます
たとえば、あなたの学年に2クラス（1組と2組）しかなかったとします。
あなたがどちらかのクラスに入ったとして、友達が同じクラスになるか、違うクラスになるかの2択なので確率は 1/2（50%） になります。
つまり、半分の確率で同じクラスになるということです！
3組のときはどうなるかな
次に、3クラス（1組と2組と3組）ある場合を考えてみましょう。
あなたはたとえば1組になったとします。友達が1組・2組・3組のうち、1組（あなたのクラス）になる確率は1/3（約33.3%）です。
クラス数が増えると、同じクラスになる確率は下がることがわかります。
4組以上のときはどうなるかな
同じ考え方で、クラス数が4つ、5つ…と増えていくと、次のように確率が下がっていきます。
4クラス → 1/4（25%）
5クラス → 1/5（20%）
6クラス → 1/6（約16.7%）
つまり、クラスが多ければ多いほど、同じクラスになる確率は低くなるのです。
同じクラスになる確率は「1/クラスの数」で表すことができます。
同じクラスになる確率(中学生向け)
中学生は場合分けを習うと思いますが、クラス替えも場合分けして考えてみましょう。
3組の場合
自分は1組～3組のどこかになります。それぞれ1/3の確率で起こります。
- 自分が1組の場合
- 自分が2組の場合
- 自分が3組の場合
自分が1組の場合を考えると、好きな人がどのクラスになるかは1組,2組,3組のパターンがあります。
自分と同じになるのは好きな人が1組のときだけなので、自分も好きな人も1組になる確率は
（自分が1組になる確率）×（好きな人が1組になる確率）＝1/3×1/3=1/9
同じように自分が2組の場合も1/9、自分が3組の場合も1/9なので、これらを足し合わせると
1/9+1/9+1/9=3/9=1/3となります。
実は場合分けして考えても小学生向けに書いた確率と同じになるのです。
同じクラスになる正確な確率（高校生以上向け）
正確に計算してみましょう。高校数学を学んでいる人なら3クラスなら1/3より少し小さくなるのではと予想できるのではないですか？
では、考えていきましょう
方法① 厳密に計算する
中学校の計算で説明したとおり、自分がどのクラスになるか関係ありません。「どのクラスであれ、好きな人と同じであればいい」という計算をおこないます。
学年の人数とクラスの人数に注目して計算していきます。
例）学年全体が160人いて40人1クラス(合計4クラス)に分ける場合
１．自分がいるクラスだけを考えます。
２．40人クラスですが、自分を除けば39人です。39人の中に好きな人が入る確率を考えます。
３．自分以外の人間から39人が選ばれます。自分以外の人数は160-1=159人です
４．159人の中にいる好きな人が39人に入ればいいので確率は39/159となります。
39/159≒0.245283なので、1/4よりもわずかに小さな確率になることがわかります。
同様に学年全体の人数をN人、クラスの数をMとしたときに一般化すると
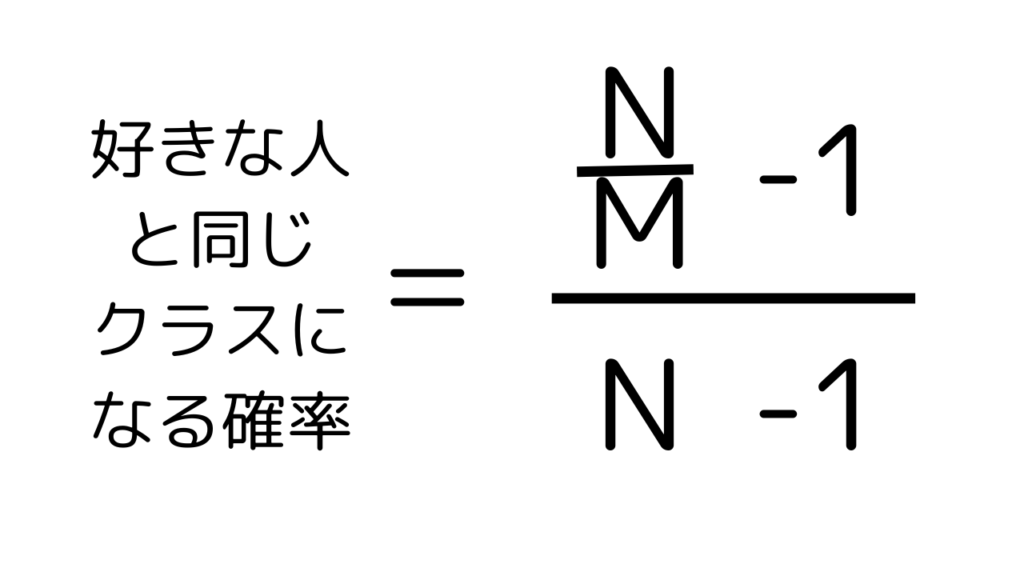
MやNに値を代入することで好きな人と同じクラスになる確率を計算することができます。
方法② 順列・組み合わせを用いて計算する
クラス分けの総通り数のうち、何通りが好きな人と同じクラスになるのかを計算していきます。
例）学年全体が160人いて40人1クラス(合計4クラス)に分ける場合
計算の全容を先に説明します。
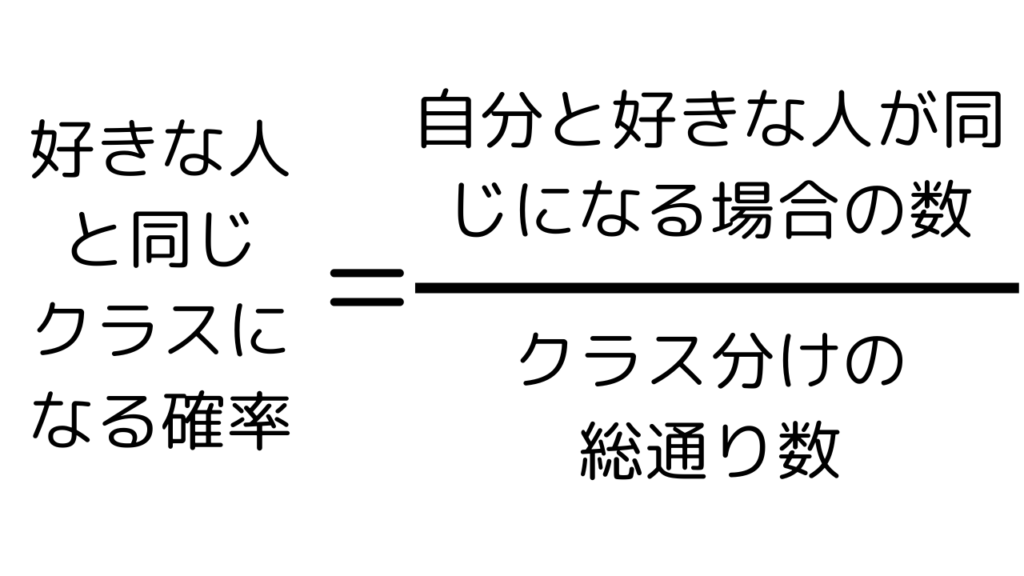
という計算をします。自分と好きな人が同じになる場合の数は
これで計算していきます。それぞれのパーツを計算していきます。
先ほどと同じ条件で、まずは順番を無視して160を40人ずつ4つのクラスに分ける総数を考えると
160!/(40!×40!×40!×40!)通りあります。
自分と好きな人が同じクラスになるのは1組～4組までの4通り存在する。
自分と好きな人が入ったクラスに残りの38人を158人から選ぶ総数は
158!/(38!×(158-38)!)通りとなります。
最後に残った120人を3クラスに40人ずつ分ける総数は
120!/(40!×40!×40!)通りとなります。
これを整理すると
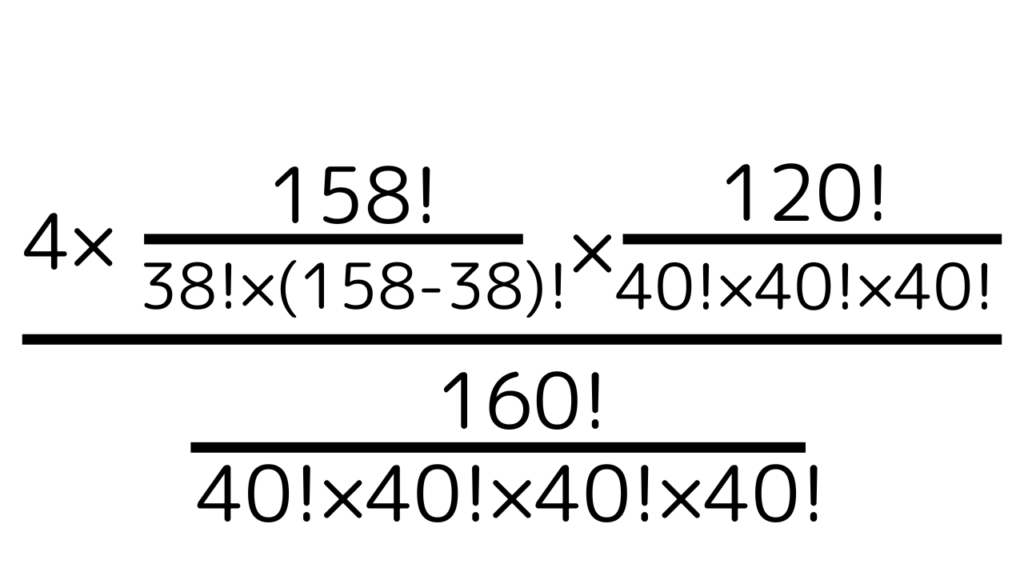
一見大変そうに見えますが、分子分母で打ち消しあうので、計算方法を工夫してみると手計算でもできそうですよ？
まとめると「39/159」見たことある数字が出てきましたね。計算方法は違えど、同じ答えになる。これが数学のすごいところ。
39/159≒0.245283なので、1/4よりもわずかに小さな値となっていますね。
さいごに
現実で考える場合、男女比やクラス替えの配慮が働くのでこんな簡単にはいきません。
同じクラスになれたのはめずらしい確率で、珍しいことなんだやったラッキーくらいの気持ちでいましょう。
「同じクラスになれなくても仕方ない」と思えるのもまた確率というのも伝えたいことです。確率大好きなんですよね。
クラス替えの方法については下記記事で解説しています。
ABOUT ME
趣味関連の最新情報や教員時代のノウハウを皆様にお届けすべく、日々奮闘中です。
趣味はAPEXLegendsをはじめとしたオンラインゲーム。ネットやパソコンが得意です。 1児の父で子育てについても発信していきます！
趣味はAPEXLegendsをはじめとしたオンラインゲーム。ネットやパソコンが得意です。 1児の父で子育てについても発信していきます！
